转载要注明作者、出处哟。
前段时间在做可以兼容J2ME和Android的ARPG引擎,获得一些心得。2D手机游戏似乎画面上没什么突破,几乎都是靠美工把地图画得华丽一些,然后加一些云朵、光晕的贴图,再弄点下雨、下雪啥的,已经见怪不怪了。看了一些前几年的PC游戏,同样是2D,像暗黑就有模拟的光照效果,场景有明暗之分,人物也阴影效果。目前手机游戏有点类似当年的形态,当然即时是现在的手机也无法与当年的PC性能抗衡。要在2D手机游戏上实现这些效果肯定要降低效果的质量。
先来说阴影,原理其实很简单,比如要给一个人物精灵绘制阴影:
1)将精灵原图按比例拉伸、旋转
2)转换成带alpha效果的黑色图片
3)绘制到人物脚下
OK!既然这么简单,立马实现到现有的游戏中去看看效果!
结果,效果是出来了,速度却慢得惊人,由于是即时绘制,在我的N85上帧速只有5~8左右,这还只是一个人物精灵的绘制,如果给每个NPC都加上阴影……嗯,你懂的。
好吧,这可是即时运算,我们得找找影响CPU发挥的瓶颈在哪:
1)图像的拉伸、旋转网上有很多算法,什么插值法、扫描法……前辈们总结了很多,这可是在虚拟机上跑,过高的时间复杂度,甚至涉及浮点运算肯定会让速度大打折扣。
2)还有,获取原图的RGB信息,经过一系列的翻转、拉伸,然后新建个动态图像,把RPG值转成黑色填进去,再调整alpha值,再贴到指定位置……这么折腾N85居然能做到5帧,太给力了!
了解了瓶颈所在,下面停止扯淡,介绍一下我的优化方法:
跳过拉伸、旋转操作,每帧都做这么大开销的操作就是手机电池也不会答应。我们可以直接扫描图像的RGB信息,扫描到非透明的RGB值时计算出对应点的位置(计算这里涉及三角函数,为了提升性能以及兼容MIDP1.0,建议用查表法)。跳过新建图像以及alpha调整的操作,我们可以预先建立好一个半透明的黑色影子图片来贴图。
coding...经过一系列的折腾,效果出来了:
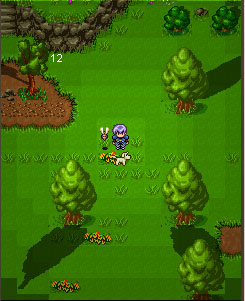 |
感觉还不错吧?场景中有4棵树绘制了阴影,N85实机帧数是20上下。(这是WTK2.5的模拟器截图,由于还开启了引擎的模拟明暗效果,所以帧数下降到了12。)
等等,N85在主流J2ME手机里算不错的,一个影子效果就让PFS降到了20,那以后加上模拟水波、模拟光照、模拟天气等等效果,不是得卡死?嗯……让我来进一步优化,不过这次可就要稍微降低一些影子的质量了:
逐个像素扫描图片,运算量也是相当惊人的,80x32的一棵小树就要判断2560次!我们可以间隔着扫描,比如扫描某行RGB信息时,扫描1个像素然后跳过下面4个像素再扫描下一个,这样影子效果可能有一些偏差,但是大致轮廓还是很清晰的。(如果扫描的像素非透明就用准备好的半透明影子图片绘制一个1x4的影子,跳过接下来4个像素继续扫描,继续绘制……)来看效果:
跳过2个像素
 |
跳过4个像素
 |
FPS提升了5倍!好吧,你应该有所启发,横向、纵向扫描越过几个像素完全由你控制,我们可以理解为扫描精度。来更进一步优化,即便是跳着扫描,仍然需要判断很多次,而我们只是要获得精灵的大致轮廓,画出阴影而已。我们完全可以从图片的两边扫描不透明点的起始位置,然后计算不透明区域的长度,根据这个长度直接贴图!
好吧,光放几张鸟图,不贴代码是不厚道的,下面是影子绘制部分的核心代码(写的比较烂,望海涵):
/** 利用透明图片绘制向下的影子
* @param g Graphics 画布对象
* @param img Image 要绘制阴影的原图
* @param px int 绘制x位置
* @param py int 绘制y位置
* @param height int 影子高度(<=原图像素高度)
* @param scanSkip int 扫描跳过的像素个数(1最高精度,建议用2)
* @param cot256 int 影子角度的cot值(这里是查表法得来的256倍)
*/
public static void drawTransShadowDown(Graphics g, Image img, int px,
int py, int height, int scanSkip, int cot256) {
int w = img.getWidth();
int h = img.getHeight();
int pels[] = new int[w];
int ofx = 0;
int scanH = 256 * h / height;
int startX = 0;
int endX = 0;
int rowIn = 0;
int scanIn = (h - 1) * 256;
g.setColor(0x000000);
while (scanIn >= 0) {
//跳过扫描?
if (rowIn % scanSkip == 0) {
img.getRGB(pels, 0, w, 0, scanIn >> 8, w, 1);
//扫描起始位置
for (int j = 0; j < w; j++) {
if ((pels[j] >> 24) == -1) {
startX = j;
break;
}
}
//扫描结束位置
for (int j = w - 1; j >= 0; j--) {
if ((pels[j] >> 24) == -1) {
endX = j;
break;
}
}
//这个方法是我自己里面封装的,类似DrawRegion,transImg是一张半透明黑色图片
BaseCanvas.drawImage(g, transImg, 0, 0, endX - startX + 1,
scanSkip, 0, px + (ofx >> 8) + startX, py + rowIn, 20);
}
ofx += cot256;
rowIn++;
scanIn -= scanH;
}
}
查表法求三角函数:
//sin(0°) to sin(90°) all *256
public final static int SIN_TABLE[] = {
0, 4, 8, 13, 17, 22, 26, 31, 35, 39,
44, 48, 53, 57, 61, 65, 70, 74, 78, 83,
87, 91, 95, 99, 103, 107, 111, 115, 119, 123,
127, 131, 135, 138, 142, 146, 149, 153, 156, 160,
163, 167, 170, 173, 177, 180, 183, 186, 189, 192,
195, 198, 200, 203, 206, 208, 211, 213, 216, 218,
220, 223, 225, 227, 229, 231, 232, 234, 236, 238,
239, 241, 242, 243, 245, 246, 247, 248, 249, 250,
251, 251, 252, 253, 253, 254, 254, 254, 254, 254,
255
};
/** 查表法求SIN值
*
* @param angle int 0到360度
* @return int 返回SIN值的256倍
*/
public static int sin256(int angle) {
angle %= 360; // 360 degrees
if (angle <= 90) { // 0..90 degrees
return SIN_TABLE[angle];
}
else if (angle <= 180) { // 90..180 degrees
return SIN_TABLE[180 - angle];
}
else if (angle <= 270) { // 180..270 degrees
return -SIN_TABLE[angle - 180];
}
else { // 270..360 degrees
return -SIN_TABLE[360 - angle];
}
}
public static int cos256(int angle) {
return sin256(angle + 90); // i.e. add 90 degrees
}
public static int cot256(int angle){
return cos256(angle)*256/Math.sin256(angle);
}
public static int tan256(int angle){
return sin256(angle)*256/Math.cos256(angle);
}
最后,有一个问题值得注意,细心观察自然界的影子,其实并不是直接旋转一下原图的效果,而是根据光源的位置投影而来的。网上有些那原图直接翻转的方法其实是错的,本文的方法也不太正确,但至少在2D游戏里看上去像那么回事,哈哈,看图为证~
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。