跳票工厂

手机平台上开发斜45度地图系统的游戏，相信做惯了正面俯视的开发者刚接触总很不习惯。所谓斜45度游戏，也就是常说的2.5D游戏，用斜方向俯视的角度来增强立体感的一种技术。这种技术在PC平台上早就流行了，手机平台由于屏幕表现力的限制，大部分使用正面视角。但随着手机屏幕分辨率不断增大，斜45度视角的游戏出现得越来越多。

斜45度地图系统分Staggered、Slide、Diamond等几种，除了起始位置的区别，与正视地图系统的主要区别在于使用菱形的图块。关于什么是45度地图系统以及其原理，我不想再多说，网上有很多的资料，下面主要讲一讲坐标系的转换。

图1

图2（该图来自云风的博客http://www.codingnow.com/）

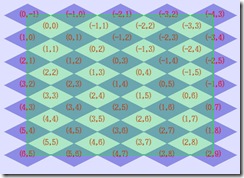
如图1，虽然图块是菱形拼接，但图片还是矩形，绘制地图就是要矩形的图片映射到正确的屏幕坐标系上，使图片无缝地拼接起来。如图2，以Diamond地图系统为例，为了简化，掠过滚屏等问题，假设始终从屏幕左上角开始绘制0,0的数据，图中所标的数字是指图块数据下标（data[j][i]中的(j,i)）。通过观察你会发现：图片的X位置为数据j,i之差乘以图片宽度的一半，Y位置为数据j,i之和乘以高度的一半，即公式1：

           px  = (CHIP_W >> 1) * (i - j);

           py = (CHIP_H >> 1) * (i + j);

通过公式1，我们就能根据数据数组的下标值获得对应图块在屏幕坐标系中的位置。逆推，得到公式2：

        i = 0.5f * (y / (CHIP_H >> 1) + x / (CHIP_W >> 1));
        j =  0.5f * (y / (CHIP_H >> 1) - x / (CHIP_W >> 1));

通过公式2，可以把图块位置映射到对应的数据坐标。

下面开始绘制地图内容。传统的俯视角度游戏地图绘制，都是记录屏幕（或摄像机）所在的数据j,i位置，计算屏幕能容纳多少个图块，用一个嵌套循环完成地图的绘制。如下所示：

         for(int j=0;j<SCREEN_HEIGHT/CHIP_H;j++)

         {

                 for(int i=0;i<SCREEN_WIDTH/CHIP_W;i++)

                 {

                      ......//do draw

                 }

          }

图3

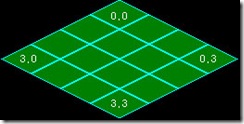
但是如图3所示，斜45度地图是斜的，无法用数组的循环遍历来绘制。不过既然有了转换公式，我们可以把屏幕分割成CHIP_W/2*CHIP_H/2的若干个区域，通过“遍历”这些区域的坐标，可以用公式知道，要在这个坐标上画哪张图片。算法如下：

Java代码：

1. //当paintY为CHIP_H / 2的奇数倍时,paintX需要偏移CHIP_W / 2   
2. int offset = 0;  
3. for (int paintY = 0; paintY <= SCREEN_H + CHIP_H; paintY += CHIP_H / 2)   
4.  
5.     for (int paintX = 0; paintX <= SCREEN_W + CHIP_W; paintX += CHIP_W)   
6.    {  
7.         int gx = getGx(paintX + offset, paintY) + startCol;  
8.         int gy = getGy(paintX + offset, paintY) + startRow;   
9.         if (gy < 0 || gx < 0 || gy > 10 || gx > 10)  
10.         {   
11.             continue;   
12.         }   
13.         drawTile(g, data[gy][gx], paintX + offset, paintY);   
14.     }   
15.     offset = offset == 0 ? CHIP_W / 2 : 0;  
16. } 
17. //当paintY为CHIP_H / 2的奇数倍时,paintX需要偏移CHIP_W / 2
18. int offset = 0;
19. for (int paintY = 0; paintY <= SCREEN_H + CHIP_H; paintY += CHIP_H / 2)
20. {
21. for (int paintX = 0; paintX <= SCREEN_W + CHIP_W; paintX += CHIP_W)
22. {
23. int gx = getGx(paintX + offset, paintY) + startCol;
24. int gy = getGy(paintX + offset, paintY) + startRow;
25. if (gy < 0 || gx < 0 || gy > 10 || gx > 10)
26. {
27. continue;
28. }
29. drawTile(g, data[gy][gx], paintX + offset, paintY);
30. }
31. offset = offset == 0 ? CHIP_W / 2 : 0;
32. }

Java代码：

1. //屏幕坐标转换成游戏坐标
2. int getGx(int x, int y)   
3. {  
4.      return (int) (0.5f * (y / (CHIP_H >> 1) + x / (CHIP_W >> 1)));   
5. }  
6.  
7. int getGy(int x, int y)   
8. {  
9.      return (int) (0.5f * (y / (CHIP_H >> 1) - x / (CHIP_W >> 1)));   
10. } 
11. //屏幕坐标转换成游戏坐标
12. int getGx(int x, int y)
13. {
14. return (int) (0.5f * (y / (CHIP_H >> 1) + x / (CHIP_W >> 1)));
15. }
16. int getGy(int x, int y)
17. {
18. return (int) (0.5f * (y / (CHIP_H >> 1) - x / (CHIP_W >> 1)));
19. }

关于地图上的碰撞与拾取。当你需要判断精灵所处地图数据位置的时候用公式2，会发现判断误差很严重，仔细想一下不难解释：逆推过来的公式是根据图片之间的坐标系来定义的，而菱形切片之间透明的部分都是重叠的，所以当你判断重叠部分的碰撞时就无法预计判断是那一块数据了，所以用公式2进行地图数据的碰撞判断不可行。

图4

图５

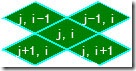
图６

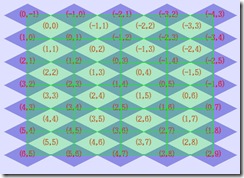
介绍一下我的碰撞方法。如图4，要判断屏幕中任意一点X,Y于数据中的位置。首先按图块的图片尺寸将屏幕分割，计算X,Y位于图中绿色矩形框选的哪个图片中，初步得到j,i。知道了位于哪张图块图片中，如图5，再判断X,Y位于图5中四个角落哪一个区域。结合图6，如果都不位于这四个角落，那X,Y就属于j,i。位于左上角的红色区域，对应i-1，其它三个角落同理。这里的难点在于如何判断红色区域，建议用三角形与点碰撞的算法。这种碰撞拾取算法的优点是精确无误差，而且无论菱形图块比例是32:15 、2:1还是其他比例都可以检测。

数据碰撞检测的主要代码：

Java代码：

1. int[] checkInDataIJ(int x, int y)  
2. {  
3.     final int I = 0;  
4.     final int J = 1;  
5.     int[] data = new int[] { 0, 0 };  
6.     Log.e("", "click:" + x + "," + y);  
7.     int xd = x / CHIP_W;  
8.     int yd = y / CHIP_H;  
9.     if (x < 0)  
10.     {  
11.         xd -= 1;  
12.     }  
13.     if (y < 0)  
14.     {  
15.         yd -= 1;  
16.     }  
17.     Log.e("", "xd:" + xd + " yd:" + yd);  
18.     data[I] = yd + xd;  
19.     data[J] = yd - xd;  
20.     //计算触摸点位于矩形中，与菱形的位置
21.     int cx = x % CHIP_W;  
22.     if (cx < 0)  
23.     {  
24.         cx += CHIP_W;  
25.     }  
26.     int cy = y % CHIP_H;  
27.     if (cy < 0)  
28.     {  
29.         cy += CHIP_H;  
30.     } //是否位于左上角的三角形
31.     if (MyMath.isInsideTriangle(cx,  
32.             cy,  
33.             new int[] { 0, CHIP_W / 2, 0 },  
34.             new int[] { 0, 0, CHIP_H / 2 }))  
35.     {  
36.         data[I] -= 1;  
37.     }  
38.     //是否位于右上角的三角形
39.     else if (MyMath.isInsideTriangle(cx, cy, new int[] { CHIP_W / 2,  
40.             CHIP_W, CHIP_W }, new int[] { 0, 0, CHIP_H / 2 }))  
41.     {  
42.         data[J] -= 1;  
43.     }  
44.     //是否位于右下角的三角形
45.     else if (MyMath.isInsideTriangle(cx, cy, new int[] { CHIP_W, CHIP_W,  
46.             CHIP_W / 2 }, new int[] { CHIP_H / 2, CHIP_H, CHIP_H }))  
47.     {  
48.         data[I] += 1;  
49.     }  
50.     //是否位于左下角的三角形
51.     else if (MyMath.isInsideTriangle(cx,  
52.             cy,  
53.             new int[] { 0, CHIP_W / 2, 0 },  
54.             new int[] { CHIP_H / 2, CHIP_H, CHIP_H }))  
55.     {  
56.         data[J] += 1;  
57.     }  
58.     Log.e("debug", "get(:" + data[J] + "," + data[I] + ")");  
59.     return data;  
60. } 
61. int[] checkInDataIJ(int x, int y)
62. {
63. final int I = 0;
64. final int J = 1;
65. int[] data = new int[] { 0, 0 };
66. Log.e("", "click:" + x + "," + y);
67. int xd = x / CHIP_W;
68. int yd = y / CHIP_H;
69. if (x < 0)
70. {
71. xd -= 1;
72. }
73. if (y < 0)
74. {
75. yd -= 1;
76. }
77. Log.e("", "xd:" + xd + " yd:" + yd);
78. data[I] = yd + xd;
79. data[J] = yd - xd;
80. //计算触摸点位于矩形中，与菱形的位置
81. int cx = x % CHIP_W;
82. if (cx < 0)
83. {
84. cx += CHIP_W;
85. }
86. int cy = y % CHIP_H;
87. if (cy < 0)
88. {
89. cy += CHIP_H;
90. } //是否位于左上角的三角形
91. if (MyMath.isInsideTriangle(cx,
92. cy,
93. new int[] { 0, CHIP_W / 2, 0 },
94. new int[] { 0, 0, CHIP_H / 2 }))
95. {
96. data[I] -= 1;
97. }
98. //是否位于右上角的三角形
99. else if (MyMath.isInsideTriangle(cx, cy, new int[] { CHIP_W / 2,
100. CHIP_W, CHIP_W }, new int[] { 0, 0, CHIP_H / 2 }))
101. {
102. data[J] -= 1;
103. }
104. //是否位于右下角的三角形
105. else if (MyMath.isInsideTriangle(cx, cy, new int[] { CHIP_W, CHIP_W,
106. CHIP_W / 2 }, new int[] { CHIP_H / 2, CHIP_H, CHIP_H }))
107. {
108. data[I] += 1;
109. }
110. //是否位于左下角的三角形
111. else if (MyMath.isInsideTriangle(cx,
112. cy,
113. new int[] { 0, CHIP_W / 2, 0 },
114. new int[] { CHIP_H / 2, CHIP_H, CHIP_H }))
115. {
116. data[J] += 1;
117. }
118. Log.e("debug", "get(:" + data[J] + "," + data[I] + ")");
119. return data;
120. }

三角形检测算法：

Java代码：

1. public static boolean isInsideTriangle(int cx, int cy, int[] x, int[] y)  
2. {  
3.     float vx2 = cx - x[0];  
4.     float vy2 = cy - y[0];  
5.     float vx1 = x[1] - x[0];  
6.     float vy1 = y[1] - y[0];  
7.     float vx0 = x[2] - x[0];  
8.     float vy0 = y[2] - y[0];  
9.     float dot00 = vx0 * vx0 + vy0 * vy0;  
10.     float dot01 = vx0 * vx1 + vy0 * vy1;  
11.     float dot02 = vx0 * vx2 + vy0 * vy2;  
12.     float dot11 = vx1 * vx1 + vy1 * vy1;  
13.     float dot12 = vx1 * vx2 + vy1 * vy2;  
14.     float invDenom = 1.0f / (dot00 * dot11 - dot01 * dot01);  
15.     float u = (dot11 * dot02 - dot01 * dot12) * invDenom;  
16.     float v = (dot00 * dot12 - dot01 * dot02) * invDenom;  
17.     return ((u > 0) && (v > 0) && (u + v < 1));  
18. } 
19. public static boolean isInsideTriangle(int cx, int cy, int[] x, int[] y)
20. {
21. float vx2 = cx - x[0];
22. float vy2 = cy - y[0];
23. float vx1 = x[1] - x[0];
24. float vy1 = y[1] - y[0];
25. float vx0 = x[2] - x[0];
26. float vy0 = y[2] - y[0];
27. float dot00 = vx0 * vx0 + vy0 * vy0;
28. float dot01 = vx0 * vx1 + vy0 * vy1;
29. float dot02 = vx0 * vx2 + vy0 * vy2;
30. float dot11 = vx1 * vx1 + vy1 * vy1;
31. float dot12 = vx1 * vx2 + vy1 * vy2;
32. float invDenom = 1.0f / (dot00 * dot11 - dot01 * dot01);
33. float u = (dot11 * dot02 - dot01 * dot12) * invDenom;
34. float v = (dot00 * dot12 - dot01 * dot02) * invDenom;
35. return ((u > 0) && (v > 0) && (u + v < 1));
36. }